サポートベクトルマシン

ホーム
技術者BLOG
サポートベクトルマシン

こんにちは。第二ソリューションの K.S です。

はじめに

今回は、サポートベクトルマシンの学習をしました。
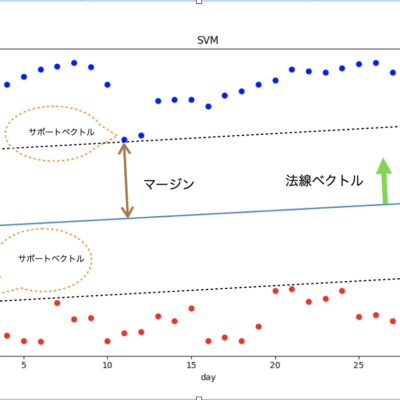
サポートベクトルマシンとは、集合Ａと集合Ｂが分布する境界を求め分類するための方法になります。
サポートベクトルマシンでも境界の求め方に何種類か方法がありますが、今回は初心者向けの線型分類(y=ax+bで集合Ａと集合Ｂの間に境界線を引きます)であるハードマージンタイプ(集合Ａと集合Ｂが境界線を跨ぐことなく綺麗に分離できる)を扱います。
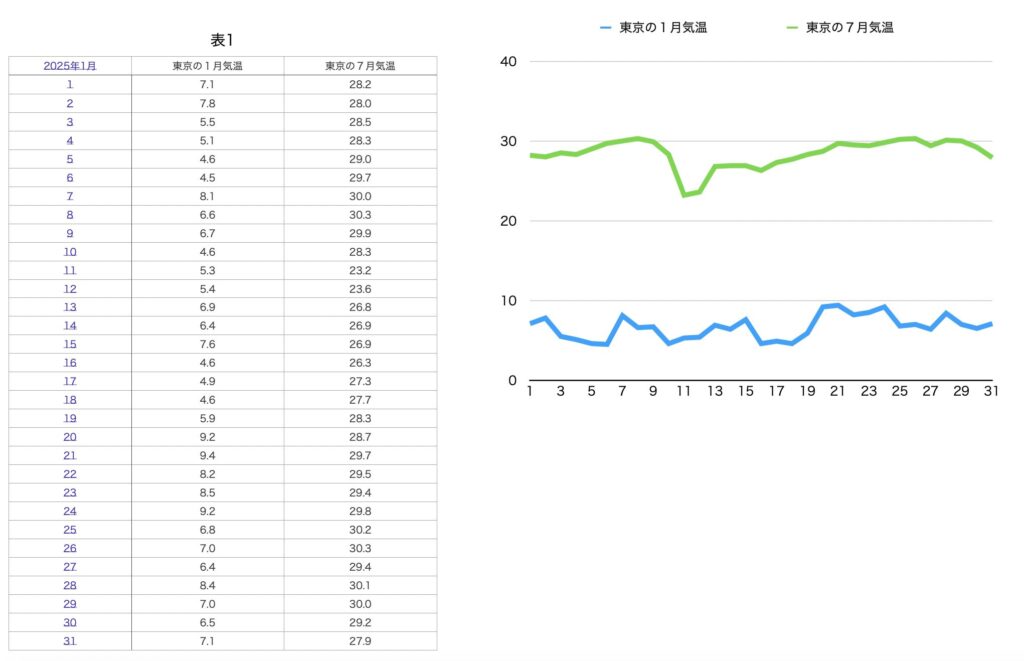
そこで選んだデータは、東京都の冬(2025年1月)と夏(2025年7月)の平均気温を使用することにしました。図を見てもわかるように、はっきりと境界が引けそうです。

サポートベクトルマシンの数学的導出方法

実用を重視しているといいましょうか、あまりスッキリした気がしませんが、どのようにして境界を求めるのかをみていきます。

\(
集合Ａと集合Ｂを分ける境界線を
\quad f(X)=0 \quad
とおくと、境界線より上にある点は
\quad f(X) > 0 \quad
境界より下にある点は
\quad f(X) < 0 \quad となります。 \) \(サポートベクトルとは集合Ａ、集合Ｂの中から各々境界線に最も近い点をといいます。また、マージンとはサポートベクトルから境界線までの距離をいいます。\) \(サポートベクトルマシンでは、このマージンが最大になるような境界線\) \[ f(x) = xw + b = 0 \quad (w は境界線の法線ベクトル) \] \(を求めます。\) \(学習データによって与えられた点 x_i(a_1,・・・,a_n) から境界線までの距離を d_i とします。\) \(この d_i は距離の公式より\) \[ d_i = \frac{|f(x_i)|}{\|w\|} = \frac{|x_i w + b|}{\|w\|} \] \(となります。\) \(学習データの点 x_i の中から d_i の最小となるサポートベクトルを探す最小化問題と、見つかったサポートベクトルのマージンを最大化する最大化問題が以下になります。\) \[ \underset{w,b}{max}(\underset{i}{min}(d_i)) \] \(また、学習データの点 x_i が境界線より上にある場合は f(x_i) > 0 となるので、これを y_i = +1 と表し、x_i が境界線より下にある場合は f(x_i) < 0 となるので、これを y_i = -1 と表します。\) これをまとめると(等号も学習データから y_i を求められるので含めておきます) \[ y_i(x_i w + b) \ge 0 \quad y_i = \pm 1 \] になり、これを制約式といいます。 \(ここで、\underset{w,b}{max}(\underset{i}{min}(d_i)) \quad を解こうとするとき、まず、\underset{i}{min}(d_i) \quad を解きますが、これを解くためには境界線が決まっていないと解けません。また、境界線の \quad w、b \quad を解くためには \quad \underset{i}{min}(d_i) \quad を先に解かなければいけないことに気づきます。\) \(そこで、サポートベクトルが |x_i w + b| = 1 に存在すると仮定して、\|w\| \quad の大きさだけの問題に単純化します。\) \[ \underset{w,b}{max}(\underset{i}{min}(d_i))=\underset{w,b}{max}(\frac{|x_i w + b|}{\|w\|})=\underset{w,b}{max}(\frac{1}{\|w\|})=\underset{w,b}{min}(\|w\|) \] \(ここでいきなり、以下のようなマージン最大化の式がでてきます。\) \((はっきり言って、\|w\| → \frac{1}{2}w^T w \quad となる理由がわかっていませんが、今は、次のラグランジェ未定乗数法を使って \quad w \quad について微分したときに消えないように \quad w \quad を積分した式を使っているぐらいに思っておきます。)\) \[ \underset{w,b}{min}(\frac{1}{2}w^T w) \] \[ y_i(x_i w + b) \ge 0 \quad y_i = \pm 1 \] \(次に、ラグランジェ未定乗数法を使用して制約付最適化問題の式を立てます。 (実はまだラグランジェ未定乗数法と双対問題の証明をちゃんと追えていません。) \) \[ L(λ, w, b) = \frac{1}{2}w^Tw - \sum_{i=1}^{N}λ_i \{y_i(x_i w + b) - 1 \} \] \[ λ = (λ_1,・・・, λ_N)^T で λ_i は学習データの各点 x_i に対応するラグランジェ未定乗数になります。 \] この式を偏微分を用いて最小解を求めます。 \[ \frac{\partial L}{\partial w} = w - \sum_{i=1}^{N}λ_i y_i x_i^T = 0 \] \[ \textbf{w} = \sum_{i=1}^{N}λ_i y_i x_i^T \] \[ \frac{\partial L}{\partial b} = - \sum_{i=i}^{N}λ_i y_i = 0 \] \( この \quad \textbf{w} \quad と\quad \frac{\partial L}{\partial b} \quad の結果を L(λ, w, b) に代入するとλの関数になります。 \) \[ L(λ, \textbf{w}, b) = \frac{1}{2}(\sum_{i=1}^{N}λ_i y_i x_i^T)^T(\sum_{j=1}^{N}λ_j y_j x_j^T) - \sum_{i=1}^{N}λ_i\{y_i x_i (\sum_{j=1}^{N}λ_j y_j x_j^T) + y_i b -1 \} \] \[ = - \frac{1}{2} \sum_{i=1}^{N}λ_i y_i x_i \sum_{j=1}^{N} λ_j y_j x_j^T + \sum_{i=1}^{N} λ_i \] \[ = - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N}λ_i y_i x_i x_j^T y_j λ_j + \sum_{i=1}^{N} λ_i \] \(したがって、ラグランジェ双対問題は以下になります。\) \[ \underset{λ}{max}(L(λ, \textbf w, b)) = - \frac{1}{2}\sum_{i=1}^{N} \sum_{j=1}^{N} λ_i y_i x_i x_j y_j λ_j + \sum_{i=1}^{N}λ_i \] \[ \sum_{i=1}^{N}λ_i y_i = 0、双対問題の制約式より \quad λ_i \ge 0 \] \(この双対問題を解くためには、学習データを代入して双対問題の式が最大になるような \quad λ \quad をコンピュータに計算させて求めます。\) \(ここで得られた \quad λ \quad を \quad \textbf{λ} \quad とし \quad \textbf{w} \quad に代入します。\) \[ \textbf{w} = \sum_{i=1}^{N}λ_i y_i x_i^T \] \(次に、b \quad の最小解を \quad \textbf{b} \quad とすると、KKT 条件の相補性とラグランジェ未定乗数法で立てた式 \quad L(λ, w, b) \quad の2項目により以下の条件を得ます。\) \[ \textbf{λ} \{ y_i (x_i \textbf{w} + \textbf{b}) - 1 \} = 0 \] \( y_i = \pm 1 より、学習データの点 x_i がサポートベクトルでない場合は、y_i(x_i \textbf{w} + \textbf{b}) - 1 \ne 0 \quad のため \quad \textbf{λ} = 0 \quad となり最小解 \quad b \quad が求まりません。 \) \( ところが、学習データの点 x_i がサポートベクトルの場合は、y_i(x_i \textbf{w} + \textbf{b}) - 1 = 0 \quad となり \quad \textbf{λ} > 0 \quad となり \quad \textbf{b} \quad が求まります。
\)
\[
\textbf{b} = \frac{1}{y} \quad – \quad x_i \textbf{w} = y \quad – \quad x_i \textbf{w}
\]
\[
ただし、y = \pm1 \quad より \quad y = \frac{1}{y}、x_i \quad はサポートベクトルとなる学習データの点
\]
\(サポートベクトルは複数存在するため最小解 \quad \textbf{b} \quad は平均となる。\)
\[
\textbf{b} = \frac{1}{サポートベクトルとなる点の個数} \sum_{サポートベクトルとなるi}(y_i – x_i \textbf{w})
\]
故に、境界線は以下の式になります。
\[
f(x) = x \textbf{w} + \textbf{b}
\]

プログラム

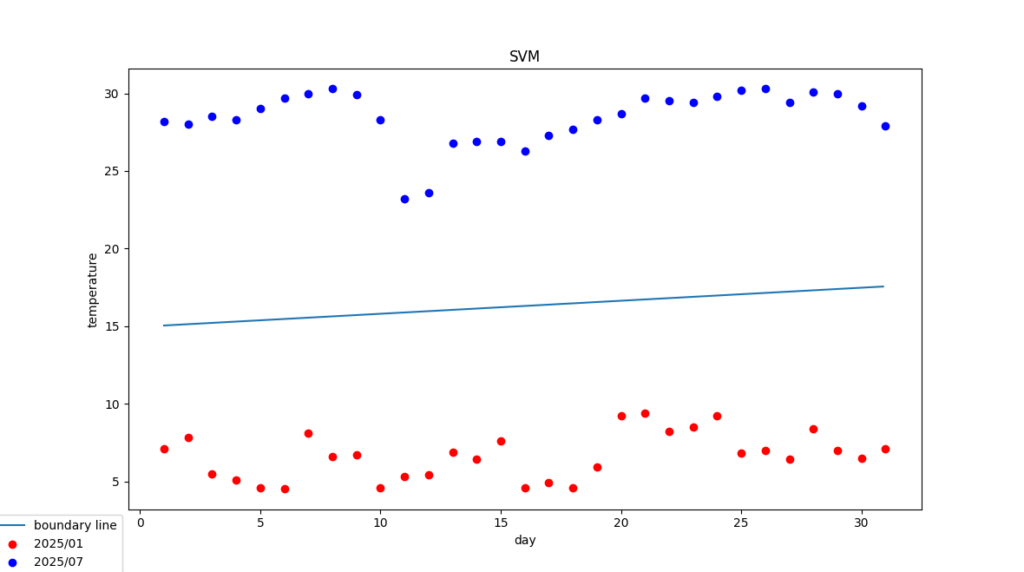
プログラムはデータファイルを読み込み境界線を求めた後、以下の東京の平均気温で冬、夏をテストしています。
2025/02/01　　7.5 　　冬
2025/02/16　　11.3　　冬
2025/08/10　　26.3　　夏
2025/08/06　　32.3　　夏

import pandas as pd import matplotlib.pyplot as plt import numpy as np from sklearn import svm

df_data = pd.read_csv(“data.csv”)

# 冬(W)に0、夏(S)に1
dx = df_data[[“日”, “平均気温”]]
dy = df_data[“季節”].map({“W”:0, “S”:1})

# 2025/02/01、2025/02/16、2025/08/10、2025/08/06 の平均気温
test_dx = [[1, 7.5], [16, 11.3], [10, 26.3], [6, 32.3]]
test_dy = [[0], [0], [1], [1]]

df_test_dx = pd.DataFrame(data=test_dx, columns=[“日”, “平均気温”])

linear_svm = svm.SVC(kernel=’linear’)
linear_svm.fit(dx, dy)

print(“テスト”, linear_svm.predict(df_test_dx))
print(“正答率”, linear_svm.score(df_test_dx, test_dy))

print(“傾き”, linear_svm.coef_)
print(“切片”, linear_svm.intercept_)

nx = np.arange(1, 31, 0.1)

# 特徴量1(日)、特徴量2(気温)のとき f1*w1+f2*w2+b=0 からf2=-(f1*w1+b)/w2
ny = (- linear_svm.coef_[0, 0] * nx – linear_svm.intercept_) / linear_svm.coef_[0, 1]
plt.plot(nx, ny, label=”boundary line”)

np_dx = dx.to_numpy()
np_dy = dy.to_numpy()

plt.scatter(np_dx[np_dy == 0, 0], np_dx[np_dy == 0, 1], c=”red”, label=”2025/01″)
plt.scatter(np_dx[np_dy == 1, 0], np_dx[np_dy == 1, 1], c=”blue”, label=”2025/07″)

plt.xlabel(‘day’)
plt.ylabel(‘temperature’)

plt.title(‘SVM’)
plt.legend(bbox_to_anchor=(0, 0))

plt.show()

CSVデータ

月,日,平均気温,季節 1,1,7.1,W 1,2,7.8,W 1,3,5.5,W 1,4,5.1,W 1,5,4.6,W 1,6,4.5,W 1,7,8.1,W 1,8,6.6,W 1,9,6.7,W 1,10,4.6,W 1,11,5.3,W 1,12,5.4,W 1,13,6.9,W 1,14,6.4,W 1,15,7.6,W 1,16,4.6,W 1,17,4.9,W 1,18,4.6,W 1,19,5.9,W 1,20,9.2,W 1,21,9.4,W 1,22,8.2,W 1,23,8.5,W 1,24,9.2,W 1,25,6.8,W 1,26,7.0,W 1,27,6.4,W 1,28,8.4,W 1,29,7.0,W 1,30,6.5,W 1,31,7.1,W 7,1,28.2,S 7,2,28.0,S 7,3,28.5,S 7,4,28.3,S 7,5,29.0,S 7,6,29.7,S 7,7,30.0,S 7,8,30.3,S 7,9,29.9,S 7,10,28.3,S 7,11,23.2,S 7,12,23.6,S 7,13,26.8,S 7,14,26.9,S 7,15,26.9,S 7,16,26.3,S 7,17,27.3,S 7,18,27.7,S 7,19,28.3,S 7,20,28.7,S 7,21,29.7,S 7,22,29.5,S 7,23,29.4,S 7,24,29.8,S 7,25,30.2,S 7,26,30.3,S 7,27,29.4,S 7,28,30.1,S 7,29,30.0,S 7,30,29.2,S 7,31,27.9,S